Contextualization

Minimax is an algorithm used in AI, decision theory, game theory and so many other fields to minimize the possible loss in a maximum loss scenario.

Originally it was developed for a n-player game covering all the possible moves. So, since it covers all the moves in a game it always get’s the best result possible in the game, making it unbeatable on all games where it can be applied. I said can be applied because in more complex games like chess where there are more moves than in the entire universe, the tree for each move is so big that it neither fit’s in memory neither is computable in useful time!

How it works?

Ok, now with the formalisms out of the way, let’s see how does this work. To begin talking about this we first need to define how is the score calculated in the game, that is a score for each move. To star simple, we will begin with the simple yet fun game of tic-tac-toe, our good old easy game.

So, in that game we have 3 outcomes possible, we either win, lose or we draw. So let’s give a win the value of 1, a draw a value of 0 and a loss a value of -1, why these values, you may ask, well we need to encourage the win situation so, we give it a larger value than a loss or a draw, but a draw is also better than a loss, so it also has a larger value than a loss, simple as that and also, let’s also give it small numbers so we can do the math really easily by hand.

So, now we have the values, how do we make the AI play? It’s really simple, for each move we can simply sum the values of the outcome (1 for win, 0 for draw, -1 for a loss) and choose the maximum value and that will be our move. Let’s see an example of an advanced game with only 2 empty spots.

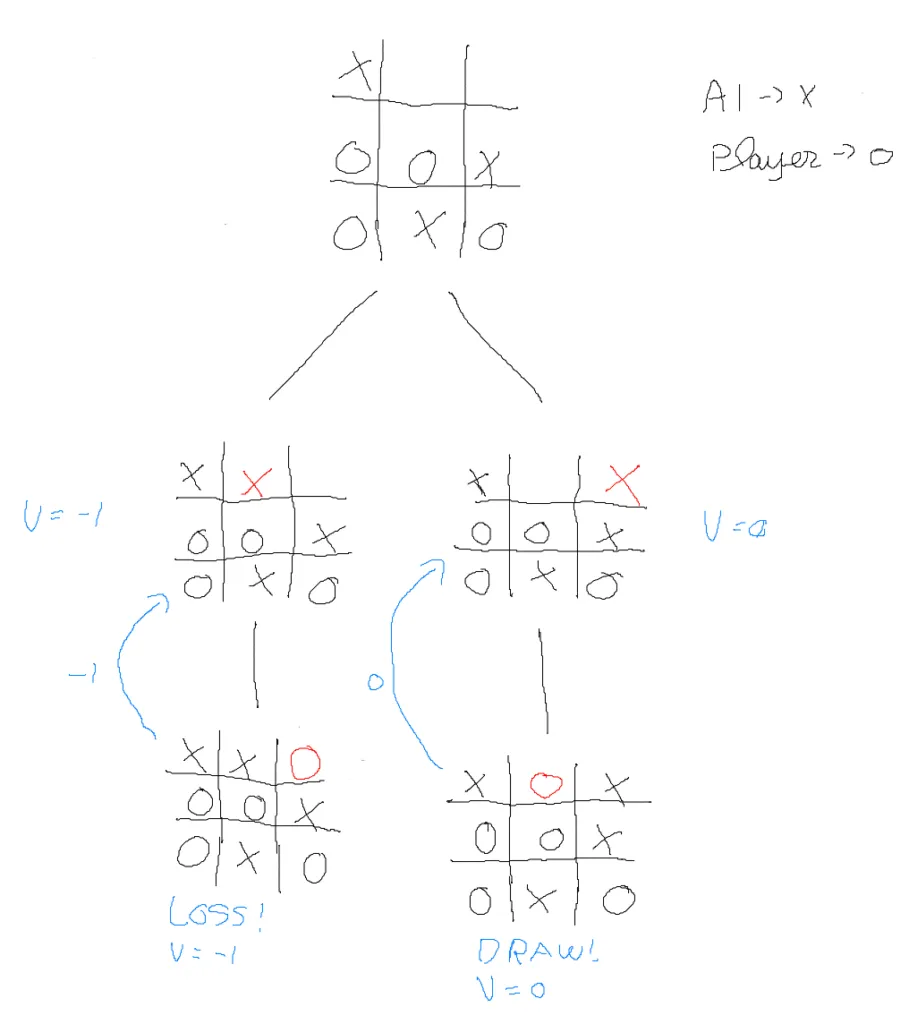
Here V represents the value of each move. So given that the leaf nodes (the last boards in the tree) have a value of -1 and 0, and they are the only children of their respective parents (the board above that is directly connected to them), the value V passes to the parent. But if the parent had more children, the value to pass would be the sum of every single children value.

So what do you think that the AI would choose if the game is at the top board? Right or left? Let’s do the math. The left one has the value of -1, the worst possible outcome (losing) is the most probable one, how do I know it? Well, aside from looking into the diagram, if the value is less or equal to the losing score (-1 in this case) then the most probable outcome is a loss if we choose that path. If the value is greater than or equal to a win value (1 in this case), then we will most certainly win if we choose that move or if the value is neutral (between -1 and 1) well, we will probably draw.

So, looking the values on the left board and on the right board in the second level of the tree, what can we conclude? Several things actually, one of them is that we will probably not win this game so we have to try and at least get a draw, so choosing the biggest value (of 0) will give us the best results concluding that in a matter of fact that the best path is indeed the right one and choosing the left one will give us a worse time.

So, I hope this helped you to understand the basis of minimax. But wait, we are not done yet! Remember about chess and me saying that applying minimax is impossible? Well there are some optimizations that we can do to improve the performance of the AI, because even for a simple game of tic-tac-toe, there are upwards of 81 possible moves! And also, us always losing is not the most fun of experiences so I will show you guys how to make the AI lose some games too! Get ready for the next section!

Optimizations

So, let’s start with a basic yet very good optimization that will let us discard entire branches of the game tree. This is called alpha-beta prunning.

This powerful technique discards the tree if the calculated value is already worse than a previous result, confusing? Example time!

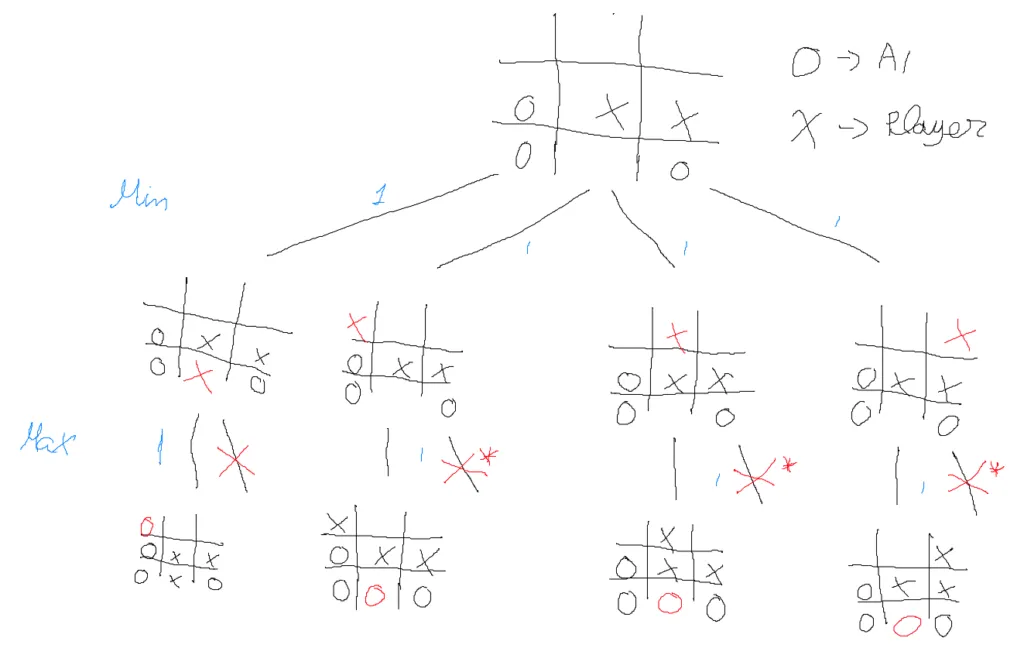
Here we can see a possible state of the game, and one thing that should pop is that we are not taking the sum of all of the possible moves, instead we check for either the maximum value or the minimum value. Why? Because it is way easier to apply this particular technique of alpha-beta pruning. Let’s see why is that.

We have 3 possible final values, right? 1 for win, 0 for a draw and -1 for a loss so if we use the maximum and minimum values we get a maximum value of 1 and the minimum value of -1, now if we do that, but with the sum, how do we know that we have reached the best result possible? Through a sum of the already known values? And then what would be the maximum value? And the minimum? Well, that is why I changed from using the sum method to check either for the maximum or the minimum. In a matter of fact, you can use whatever method to aggregate the values, some are easier other are harder.

And now how do I know if we need to maximize or minimize, well that is actually simple. If we are making a move, we want to maximize our chances to win and if the opponent is playing he wants to minimize our chances of winning and therefore maximize our chances of losing. So if we want to maximize the chances of winning, we use the function max and we use the function min if we want the opposite.

Putting all together, if we want to win, we use the function max and the maximum value we get is a 1. If the opponent wants us to loose, we use the function min and we minimize the result.

Therefore, getting a value of 1, $\beta$, on a branch that we are maximizing enables us to discard all other branches because we cannot get a higher value else if we get the minimum value of -1, $\alpha$, in a minimizing branch, we can also discard the other branches, that situations are the asterisks in the figure above.

So that is how alpha-beta pruning works, being the $\beta$ the largest value and $\alpha$ the minimum value in the branches.

Let’s also win some games

This algorithm only allows the AI to either win or draw, not to loose. A suggestion I have to allow the AI to loose is to choose the best result randomly, that is, we either choose the best move or not.

Conclusion

That’s it folks! In this article we dived deep into the Minimax Algorithm and an optimization that can be made to improve it’s performance. Thanks for reading and have a nice day!