A Leidenmayer System or a L-System consists on a set of production rules, an alphabet a string and an initial axiom. This is an iterative process that grows a string replacing the elements in the string with the productions of those elements.

This system has it origins in the University of Utrecht, in Netherlands in the hands of a botanist and theoretical biologist named Aristid Leidenmayer. Hence the name of this system.

This kind of systems are thus heavily used on biology to create realistic models of natural patterns.

Leidenmayer Systems also can create self-similar fractals through some sets of rules, but they are not limited to that.

In fact the possibilities are endless, from mathematics to creating realist plants for games.

What makes a l-system?

This system is a type of formal grammar, meaning that it follows a strict grammar, though there are variations that use a stochastic approach to create variations of the same output with the same set of rules.

But first, let’s see how does a regular system works, let’s start with the initial axiom.

The initial axiom is the initial state of the system, it is made of one or more symbols contained in the alphabet. This initial axiom is then further processed with the grammar to produce a string that is then feed back to the system, think of this like a feedback system.

A string is no more than the grammar applied over and over again to a set of symbols, starting with the axiom.

When I am speaking of alphabet, I am referring the full set of symbols that can appear in the final string.

How to build a L-System?

As example I will show how to build a Fibonacci sequence using a L-System. Don’t worry, it is not hard at all!

Let the alphabet be the letters A and B and the starting axiom the letter A. And for the grammar A turns into AB and B turns into A. Simple as that! See my drawing below on how the system evolves over each iteration.

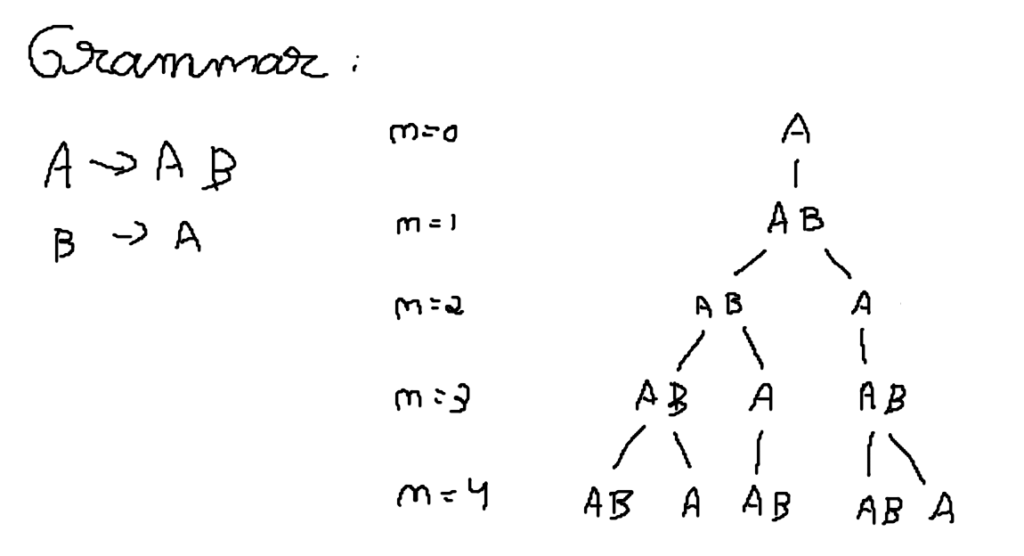
I have laid the substitutions in a tree to be easier to visualize and I have also numbered the iteration (n) at the left of each level.

Do you notice something? Count the number of nodes in each level, you will then see the Fibonacci sequence emerge and every level has as many elements as the 2 previous ones, combined!

For me that is incredible that such a simple rule set can produce such beautiful and powerful sequence.

Anyway, enough rambling about, if you notice, I applied several rules at the same time and that is fine and, as a matter of fact you should apply as much rules as you can and you cannot expand a production twice in a row, meaning that if you expanded A you cannot expand, in the same iteration, the result (AB).

Final words

I could give you endless examples of awesome l-systems, but the time is finite and as such, I will give some ideas to stimulate your creativity.

Don’t be limited by using binary trees to represent the l-system, as I did! You can choose any form to represent that and the way games represent their organic structures using l-systems is using a mapping between a symbol and a action.

For example, you could say A is go left, or B is turn right and then draw a state using that mapping. But this is just an example, feel free to think outside of the box!

Well with that, I conclude here my little peek at l-systems and I hope you liked as much as I did. See you next time!