Understanding Recursion: A Comprehensive Guide for Programmers
I. Introduction A. Definition of recursion Recursion can be stated as follows: when a process or concept requires itself to be defined.
Nowadays, Google is a giant on the internet, being youtube and dozens of other services. And all of those services rely heavily on providing suggestions to users, be it a video or a website.
One of the algorithms used by Google was Page Rank. This algorithm measures and quantifies the importance of a given page.
While is certainly not the only algorithm used by Google, is undoubtedly one of the first and the most well-known.
How it works
Page Rank or PR receives a set of pages and outputs a probability for each page to be reached given a starting point given that we follow random links at each page.
The probability given by Page Rank is not a theoretical value; instead, it is an approximation of such value, since it uses the concept of iterations to limit the otherwise infinite random walk.
This means that a higher number of iterations will approach the theoretical value more and more, although with diminishing returns.
Overview of the algorithm
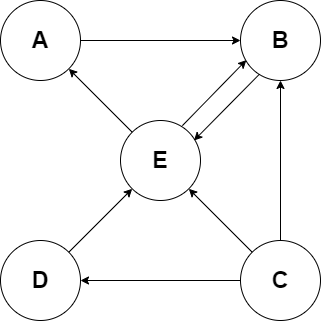
Assuming a small universe of only 5 objects: A, B, C, D, and E. And where links to itself or multiple links to another page are ignored.
Look now at the following diagram, where each circle represents one of the pages and the arrows represent a link from one page to another.
The page rank has a distribution of values between 0 and 1 and since there are 5 pages, each page will get a 20% chance at the beginning of the algorithm.
To calculate the PR of a page we use the following formula, where N is the number of pages and d is the dampening factor.
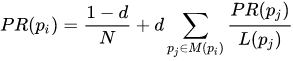
From Wikipedia
The dampening factor is a probability between 0 and 1 and represents how likely it is to continue the random walk.
Another important matrix is L, the matrix that holds the link probabilities.
The Power Method is commonly used over the iterative method to calculate the sum since it can be easier to break if we already have a “good enough” solution.
This will be the equation that will be used since it is already modified to apply the Power Method and implements an optimization to prevent errors that will be talked about later on.
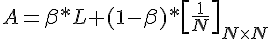
Where A is the exponent of X, being X a matrix 1 by N and whose sum is 1. This matrix X will initially have each value set equally.
And beta is a value that creates a more natural random walk. This parameter will be assumed to be 0.85 for now, and later on, explained.
Power Method
The Power Method works by multiplying a matrix by itself over and over until the difference is not significant.
This is similar to how we understand the powers of a number.
To calculate the power of a number we multiply the previous result by the number itself. Here the difference lies in the fact that we are working with matrices.
The Power Method can be applied, in this case, in 2 simple-to-follow steps.
Step 1: Getting L, A, and X
Getting X is as simple as creating a matrix whose values are one and dividing each value by the number of pages.
With the beta parameter set to 0.85 and the remaining variables being known, we then calculate A.
Step 2: Applying the Power Method
Applying the Power Method is simple.
Having the X and an epsilon (a very small value greater than 0), we start looping and checking whenever the new X is different enough (the difference is smaller than the epsilon).
If not, set the old one to the new one.
In python, one would write like this the Power Method section.
epsilon = 1e-6
while True:
new_X = A @ X
if np.max(np.abs(new_X - X)) < epsilon:
break
X = new_X
Solving our problem
Calculating the matrices
To be able to calculate the Page Rank we have 3 matrices, the link matrix, the Page Rank matrix, and the output or result matrix.
We would start by choosing a beta value, but since it is an optimization I will leave it for later.
Start by calculating the Link matrix. To do that we will assume that the rows and columns are ordered alphabetically.
So, remembering that the sum of every row of a given column is 1, we would get the following matrix:
Now we can calculate the output matrix by creating a column matrix with all values set to 1/N or 0.2.
Writing the python code
This is the code I wrote to do the calculations. It is commented on for better understanding.
import numpy as np
# the problem information
N = 5
beta = 0.85
X = np.ones((N, 1)) / N
L = np.array([[0, 0, 0, 0, 1 / 2],
[1, 0, 1 / 3, 0, 1 / 2],
[0, 0, 0, 0, 0],
[0, 0, 1 / 3, 0, 0],
[0, 1, 1 / 3, 1, 0]])
# calculate the page rank matrix
A = beta * L + (1 - beta) * np.ones((N, N)) / N
# apply the power method
epsilon = 1e-6
while True:
new_X = A @ X
if np.max(np.abs(new_X - X)) < epsilon:
break
X = new_X
print(X)
Problems and solutions
There are 2 major problems when applying this algorithm.
What if a page does not have any links or what if two pages only link to each other?
The first problem stated above is called a dead-end and the second is called a spider trap.
Dead-end Pages
A page is considered a dead-end if it does not contain any links.
This poses a problem since the sum of a column (or more) is no longer 1, meaning that the matrix is no longer stochastic.
To solve this, we can add the following code to change the matrix in such a way that whenever the sum of a column is 0 (not stochastic) all values in the column are changed to 1/N.
# turn the link matrix into a stochastic matrix
for i in range(N):
if np.sum(L[i]) == 0:
L[i] = np.ones(N) / N
This way, every time the random walk reaches a point where it can’t go anywhere, it “teleports” to a random page.
Spider traps
In spider traps, the walk is trapped between 2 or more pages without a way to reach any other page.
The solution is, as before, to teleport to a random page, randomly.
This mimics the real-life behavior of someone surfing on the web since that person can go to a completely different page and not follow any links inside that page.
To achieve this behavior, we can adjust the beta value mentioned before.
The parameter beta indicates how probable is a person to follow a link inside the current page. And, as such, we have a probability of 1-beta to teleport.
Conclusion
In conclusion, Page Rank remains a crucial component of search engine algorithms, even after more than two decades since its inception.
The algorithm’s ability to accurately assess the relevance and importance of web pages has been key to its continued use by search engines like Google.
While Page Rank has evolved over the years to account for new factors and changes in the online landscape, its core principles remain the same.
By considering the quality and quantity of links pointing to a website, Page Rank helps search engines determine the most relevant and trustworthy results to show users.
Understanding Page Rank and its role in search engine optimization is an essential aspect of digital marketing and website development.
The code used is the one below.
import numpy as np
# the problem information
N = 5
beta = 0.85
X = np.ones((N, 1)) / N
L = np.array([[0, 0, 0, 0, 1 / 2],
[1, 0, 1 / 3, 0, 1 / 2],
[0, 0, 0, 0, 0],
[0, 0, 1 / 3, 0, 0],
[0, 0, 1 / 3, 1, 0]])
# ensures the matrix is stochastic
for i in range(N):
if np.sum(L[i]) == 0:
L[i] = np.ones(N) / N
# calculate the page rank matrix
A = beta * L + (1 - beta) * np.ones((N, N)) / N
# apply the power method
epsilon = 1e-6
while True:
new_X = A @ X
if np.max(np.abs(new_X - X)) < epsilon:
break
X = new_X
print(X)