Today we will look at a algorithm for a future project that involves computer vision. The algorithm chosen is the HOG algorihtm. Let’s learn about it.

A Histogram Oriented Gradient (HOG for short) is a object detection algorithm heavily used in computer vision and image processing.

The essential of this algorithm is that the shape and the appearance can identify the object and, more importantly, that can be described by a distribution of intensity gradients or edge directions.

This set of intensity gradients and edge directions is called a descriptor.

How it works?

First, we divide the image into small yet connected regions then, a set of histogram of gradient directions is computed for the pixels of each cell (region) and finally the descriptor is calculated bu concatenating those histograms.

To improve accuracy, we can normalize the contrast of that cell, by calculating a measure of the intensity of a region larger than the current cell.

implementation of the descriptors

Now that we have a rough understanding of the HOG descriptors, I will try to explain how to calculate those descriptors in python.

Assuming that you have your image in gray scale with values ranging from zero to one, we do the following steps.

First, we calculate the gradient of the image by either subtracting the points above and below (in case we are calculating the x component of the gradient) or the image values at the left and right. In case of out of bounds, we set the value that is out of bounds to 0.

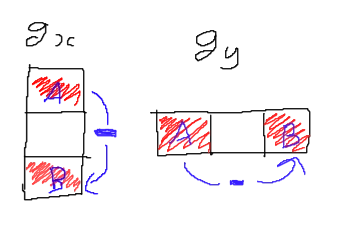
After this step, we can compute the magnitude and angle of the gradient vectors, basically converting from cartesian to polar coordinates.

In this step we need to have attention to check if gx is 0, because if it is 0 we can’t apply the formula below and instead we need to set the angle to 0.

Here is the formula to convert those coordinates from cartesian to polar.

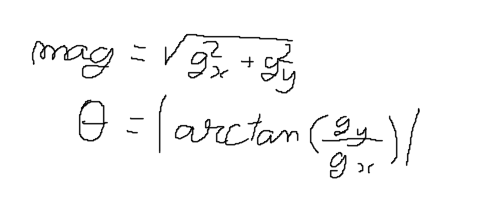
We then reach the meat of the algorithm. In here we calculate the histogram with 9 bins of those gradients for a block size of 8.

The histogram is said to have 9 bins because it has 9 slots to fit values. And the block size means that we take a portion of 8 by 8 values from the magnitude and angle vectors calculated in the previous step.

The histogram has 9 buckets of angles, ranging from 0 to 180 degrees and accordingly to the angle we distribute the magnitude values in the corresponding bins.

if the next bin exceeds 9 (the number of our bins) we wrap around and assign add the value to the first bucket or bin. To calculate the bin I am using the following formulae.

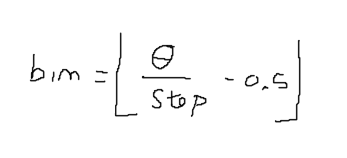
Then to calculate the weights the formula is almost the same. In the picture below I have written the formula, where b is the current bin and b + 1 is the next bin.

The assignment of the value to the bin needs to be done in a circular way so the b + 1 don’t exceeds the number of bins and instead wrap around.

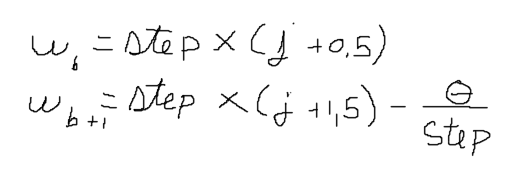
We then can multiply those weights with the magnitude and we have the values to add to the histogram.

Finally, to calculate the descriptors, we just have to normalize the histograms in block, meaning that we grab a grab a bigger window of, let’s say, a 2 by 2 histogram block, normalize, move forwards by 1 histogram, and so fourth until you reach the end. And you have the basic HOG algorithm working!

Code

The code is available on github. In there you will found the implementation by me in python and a digit recognition system based on the MNIST Number Dataset and Support Vector Machines.

I can reach about 93% accuracy which is not bad considering a first attempt using this algorithm though there are points to improve, since the scikit version of HOG with the same training images and SVM can reach upwards of 97% accuracy.

The code can be found in github here.